728x90
반응형
저자:
- Ziming Mao, UC Berkeley
- Kiran Srinivasan, NetApp
- Anurag Khandelwal, Yale
초록
- 다중 속성값을 지닌 기계 생성 데이터의 급증에 따라 대용량 데이터의 효율적인 저장과 빠른 속도의 실시간 쿼리의 기능을 가진 성능 좋은 데이터 표현이 필요함.
- 기존의 시스템들은 쿼리 속도와 공간 중 하나를 타협해서 사용하고 있음.
- 코디네이터, 스토리지 서버로 구성된 TRINITY 시스템으로 다중 속성 데이터를 효율적으로 처리시킬 수 있음.
다중 속성 데이터
- 기계 생성 데이터의 특징 : 기계 생성 데이터는 여러 속성으로 구성된 구조화된 레코드들로 이루어져 있음.
- 고유 식별자는 기본 키(primary key)로, 이를 통해 조회, 삽입, 삭제 등의 포인트 쿼리 사용 가능
- 고유 식별자를 제외한 다른 속성들을 통해 범위 쿼리나 필터 쿼리 사용.
저장 시스템의 주요 요구 사항
- 저지연 다중 속성 쿼리 : 매우 작은 시간 이내에 다중 속성 쿼리를 처리할 수 있어야 함.
- 공간 효율적 데이터 표현 : 원본 데이터셋의 크기와 작거나 같은 데이터 표현방식을 사용.
- 고처리량 포인트 쿼리 : 매우 작은 시간에 많은 포인트 쿼리를 처리해야 함.
이러한 요구사항을 만족시키기 위해 TRINITY 시스템을 설계함.
MDTRIE 데이터 구조
Morton 코드
다중 속성의 범위 쿼리를 처리하기 위해, 여러 속성의 값을 교차하여 하나의 속성으로 압축할 수 있는 Morton 코드 방법을 사용함.
- morton 코드는 다차원 공간에서 가까운 점들을 매핑함으로써, 공간적 지역성을 유지할 수 있음.
- n 차원의 데이터를 Z-순서 공간 충족 곡선(그림의 회색 선)에 따라 정렬

- 각 좌표값(y, x)을 비트로 표현 후, 특정 위치를 좌표 비트값의 교차로 표현함.
예를들어 (1, 2)를 표현하면 y=01, x=10 이고 이를 교차하여 0110 로 표현 가능.
간결한(succinct)트라이
트라이의 접두어 중복과 비트 벡터로 트라이를 표현해서 저장 공간의 효율성을 높임.
- 기존의 morton코드로 인코딩 된 값을 트리 기반 데이터에 단순히 저장하면 트리가 포인터를 많이 사용하기 때문에 저장공간이 비효율적.
- 때문에 엣지를 포인터 대신 비트로 인코딩
- 차수가 d인 노드(자식 노드의 수가 d)는 d개의 비트를 가진 벡터로 표현되고, 각 비트는 해당 자식 노드가 존재하는지 여부를 나타냄.
K2-Trie
- 4진 트리로, 각 노드가 네 가지 자식을 가질 수 있고, 각각 4비트로 인코딩됨.

- 그림의 0번 노드는 첫번째, 네번째 자식만 지니므로 ‘1001’로 인코딩.
- 자식 노드로의 각 edge는 [00, 01, 10, 11]로 구성.
- 리프노드까지 edge를 따라 연속적인 비트를 할당했을 때 L1의 코드 = 00 01 10
트리블록 구조
트라이에 새로운 데이터 포인트를 삽입하려면 많은 벡터 비트를 이동시켜야 함.
- 트라이의 일정한수의 노드를 초과하지 않게 분할시킴
- 분할시킨 트라이를 ‘트리블록’으로 만듦

- 트리블록 1의 임계값을 초과해서 새로운 트리블록인 2를 만들고, 부모 트리블록 1에 프론티어 노드(2번 노드)를 추가하여 새로운 트리블록을 가리키도록 만듦.
- 트리블록은 프런티어 노드 배열을 통해 이런 포인터들을 추적함.
Morton 코딩의 일반화
- 실제 데이터는 비트 너비[값을 표현하는데 필요한 비트 개수]가 다양한 속성들이 포함되어 있음. 기존의 morton코딩 방법은 모든 속성들의 차원을 동일한 비트 너비를 가질 수 있게 0 비트를 padding 해야해서 공간이 비효율적
- 이를 일반화 하기 위해, 특정 차원의 비트가 모두 소진되면 해당 차원의 비트를 건너뜀.

- 그림에서 (7, 1, 2)를 인코딩하는데, 기존 방법의 경우 2번째, 3번째 차원의 비트 값은 비트 너비가 각각 1, 2이므로 비트너비를 3으로 만들기 위해 0을 패딩.
- 일반화한 경우, 첫번째 교차에서는 세 차원 모두 비트를 추출하고, 두번째 교차에서는 첫번째, 세번째 차원에서만 비트를 추출, 마지막에는 첫번째 차원에서만 추출함.

- 그러면 (7,1,2)의 코드는 111 10 1으로 트라이의 첫번째 계층은 2^3개의 비트를{000~111}, 두번째, 세번째 계층은 각각 2^2{00~11}, 2^1{0, 1}개의 비트를 가질 수 있음.
- 같은 방법으로 (1, 0, 1)을 인코딩 하면 기존의 방법으로는 000 000 101이지만, 일반화한 방법을 통하면 000 01 1이 됨
- 트라이의 특정 level에서 사용되는 차원{데이터에서 비트를 추출하는 차원}을 “활성 차원”이라고 함.
압축노드
- 다중 속성의 데이터셋을 표현하는 MDTRIE의 경우, 대부분의 노드가 자식 노드를 하나만 가지고 있음.
- 특정 노드의 활성차원이 n개일 때, 1 하나 찾자고 2^n개의 비트를 저장하는건 비효율적
- 이를 최적화하기 위해 노드 표현을 2^n 비트에서 n비트로 압축해 자식 morton 코드 표현을 값(정수)으로 직접 인코딩함.
- 위 그림의 Collapsed을 보면 3번 노드는 활성 차원이 2개이므로(첫 번째 차원과 세 번째 차원의 비트만 추출), 일반화 방법으로는 2^2인 4개의 비트표현이 필요한데 이를 2개의 비트를 통해 ‘2’번째 자식을 가지고 있다는 ‘10’을 저장.
- 각 트리블록 마다 별도의 비트 벡터를 저장해놓고, 새로운 자식을 추가해야할 때는 노드의 표현을 다시 2^n 비트로 확장.
- 예를 들어, 기존에 3비트 morton 코드인 (010)이 저장된 상태[즉 2번째 자식을 지닌 상태] 에서 (101)를 추가해야 할 때, 우선 (010)비트를 8비트로 확장(00100000)
- 새로운 자식인 5(101 값)에 대한 비트를 추가로 확장시켜 morton 값을 (00100100) 으로 저장.
지연된 인코딩
- morton 코딩시, 모든 차원의 첫 번째 부터 교차할 필요가 없음. 순서대로 교차하면 지연된 차원들(1을 추출하지 못하는 차원)에서 0을 padding하는 경우 생김.
- 초기화 할때, 트라이에서 각 레벨의 활성 차원 집합만 계산하면 됨.

- 그림처럼 (왼쪽에서 오른쪽 그림방향) 활성 차원의 수를 트라이의 여러 레벨에 균형있게 조정해서 저장 효율성을 최대화 할 수있음.
- 최대화는 그리디 알고리즘 적용.
다차원 범위 쿼리
MDTRIE의 노드 가지치기를 통해 쿼리를 최적화할 수 있음.
- 각 레벨에서 활성 차원의 개수와, 각 노드의 n비트 morton 코드의 접두사를 파악할 수 있으므로, 검색 범위에서 포함되지 않는 범위를 뛰어넘을 수 있음.
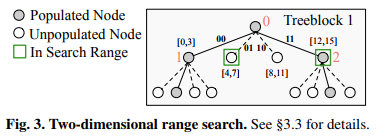

- 2<=x<=3, 0<=y<=3의 범위 탐색의경우 morton 코드에서 4~7, 12~15이고, 0~3, 8~11에 해당하는 노드의 접두사는 각각 00, 10임.
- 포함되지 않는 00, 10을 표현하는 루트 노드의 0번째와 2번째 노드는 방문하지 않으면 됨.
자가 인덱싱을 통한 포인트 쿼리
자가 인덱싱
- morton 코드는 여러 속성의 비트를 교차시켜 인코딩하기 때문에 기본 키를 기반으로 하는 포인트 쿼리를 사용하기 어려움.
- 메타데이터 (포인트 쿼리를 수행하는데 도움을 주는 데이터)를 트라이 구조에 포함시켜 비트연산을 통해 데이터 포인트를 재구성함.
- 포인트 쿼리를 위해 추가적인 인덱스를 사용하지 않아도 됨.
기본 키 저장
- 각 잎 노드에 기본 키 배열을 저장, 그리고 잎 노드 배열에 대한 포인터를 트리 블록내에서 또 다른 배열에 저장함.
기본 키로 데이터 포인트 검색
- 여러 노드가 하나의 트리블록 비트 벡터에 함께 인코딩 되기 때문에, 새로운 노드가 추가될 때마다 노드의 위치가 변경될 수 있음.
- MDTRIE는 포인터 기반이 아니기 때문에, 기본키와 잎 노드간의 연결을 유지하는게 불가능함.
- 따라서 기본 키에서 해당 잎 노드를 포함하는 트리블록에 대한 해시 기반 매핑을 저장.
- 트리블록을 거슬러 올라가며 morton 코드를 디코딩하기 위해 각 트리블록 에서 부모 트리블록으로의 역방향 포인터와 부모 트리블록의 노드 인덱스를 사전에 저장해둬야 함.
- 탐색 과정
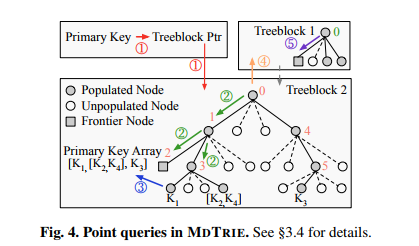
- 기본 키를 통해 해당 잎 노드를 저장하는 트리블록을 매핑을 통해 찾음.
- 트리 블록의 루트에서 잎 노드까지 DFS를 통해 경로를 추적하고 잎노드에서 기본키 탐색.
- 찾으면 탐색 종료 후, 잎 노드까지 경로를 통해 루트 노드로 역으로 올라가며 morton 코드 디코딩
- 루트까지 갔는데 현재 트리블록이 프런티어 노드일 경우, 사전에 저장해뒀던 부모 트리블록의 포인터와 프런티어 노드 인덱스를 따라감
- 부모 트리블록의 루트까지 올라가며 morton 코드 디코딩
삽입과 제거
데이터 포인트 삽입과정
- 우선 트라이에 Morton으로 인코딩된 노드를 삽입해야 함
- 트라이를 따라 내려가다가 삽입해야 하는 지점에서 자식 노드의 공간을 확보 후, 노드의 수에 따라 프런티어 노드를 생성.
- 새로운 프런티어 노드가 생성되면 부모 포인터와 프런티어 노드 인덱스 저장.
- 잎 노드에서 삽입하는 기본 키를 트리블록의 기본 키 배열에 삽입 후, 기본 키에서 트리블록으로의 매핑 추가
삭제 과정
- 삽입 과정과 비슷하게, 삭제하려는 잎 노드를 찾은 후 기본 키 제거.
- 제거한 포인트가 해당 잎 노드의 마지막 데이터 포인트일 경우, 부모노드에서 해당 비트를 지우고, 부모 노드의 자식이 없으면 부모노드도 삭제함
TRINITY 아키텍처
- 두 가지 주요 구성요소인 코디네이터와 저장 서버로 구성
- 기본 키의 해시를 기반으로 MDTRIE 샤드에 분할.
- 분할을 통해 검색 쿼리의 효율성을 높이고 병렬 처리로 조회 처리량을 증가시킴.
코디네이터
- TRINITY는 각 테이블의 데이터를 여러 MDTRIE 샤드에 걸쳐 분할
- 코디네이터는 각 저장 서버가 관리하는 MDTRIE 샤드를 매핑하고 관리
저장 서버
- MDTRIE 샤드 저장, 각 샤드에 대한 쿼리를 처리하는 쿼리 핸들러 운영
- 쿼리 실행은 병렬로 처리해서 처리량이 높음
728x90
반응형
'논문 리뷰 > 데이터베이스' 카테고리의 다른 글
| Trinity 데이터베이스 예제 실행 (0) | 2024.11.05 |
|---|---|
| [논문 리뷰] A New Method To Index And Store Spatio-temporal data (0) | 2024.10.10 |
| [논문 리뷰] k²-Trees for Compact Web Graph Representation (1) | 2024.09.16 |