저자
- Nieves R. Brisaboa, Susana Ladra (University of A Coruña, Spain)
- Gonzalo Navarro (University of Chile, Chile)
초록
- 기존에 사용하던 WWW 웹 구조의 시간적, 공간적 비효율성을 개선하기 위해, 웹 그래프를 표현하는 인접 행렬에서 넓고 빈 영역을 효율적으로 표현하여, 압축 트리 구조를 기반으로 웹 그래프 표현 방법을 제시함
- 이 논문의 방법은 그래프의 관계를 비트로 표현 하고 유사한 비용의 정 방향 탐색과 역 방향 탐색 방법을 통해 빠른 탐색 시간을 가질 수 있음.
WWW 웹 구조
- WWW 웹의 구조는 페이지 간의 하이퍼링크로 구성된 방향성 그래프로, 이 관계를 인접 행렬로 표현.
- 인접 행렬 A의 요소 A(i,j)는 i 페이지에서 j 페이지로의 하이퍼링크 유무를 나타내며, 하이퍼링크가 존재하면 1, 존재하지 않으면 0으로 표현.
WWW 웹 구조의 단점
- 그래프의 크기가 너무 커서 메인 메모리에서 사용하기 어려움.
- 그래서 보조 기억 장치에서 사용을 하려고 해도 보조 기억 장치에 저장된 웹 그래프 데이터를 탐색할 때, 기존 알고리즘들은 메모리 접근속도가 느리고 탐색 시간이 길어 비효율적.
WebGraph 압축 방법
- 통계적 특성을 활용해 링크당 2~6개의 비트로 표현 가능.
- 특징.
- 파워 법칙 분포(Power-law distribution of indegree and outdegrees) : 웹 그래프에서 각 페이지의 들어오는 링크와 나가는 링크의 수가 특정 분포를 따르는데, 소수의 페이지는 상대적으로 많은 링크를 가지고, 대부분의 페이지는 상대적으로 적은 페이지 링크를 가지는 특징
- 공간적 지역성(locality of reference) : 인접한 페이지들이 지리적으로 혹은 주제적으로 밀집되어 있는 특징
- 복사 속성(copy property) : 한 페이지가 다른 페이지의 링크 구조를 복사하는 경향. 여러 페이지가 동일한 외부 사이트로 링크를 걸면 그 외부 사이트의 링크 구조가 복사되는 특징
Re-pair 압축 방법
- 웹 그래프의 특성을 모두 만족하고 웹 그래프와 비교해 공간, 시간적 효율성이 뛰어남.
- 웹 그래프에 비해 정방향 탐색에서 더 나은 성능을 보이며, 이는 HITS, PageRank와 같은 페이지 랭크 알고리즘에 효율적임.
- 하지만 특정 상황에서 WebGraph의 성능을 크게 상회하지 못하는 경우 역시 존재.
k²-Tree의 특징 및 장점
- 특정 웹 그래프에 맞춘 기술이 아닌, 다양한 유형의 그래프에서 클러스터링(인접한 항목들이 묶이는 특성)을 활용할 수 있는 보다 일반적인 방법을 제안
- 행렬의 sparse한 특징 (넓은 빈 공간)을 효율적으로 나타낼 수 있음.
- symmetric한 특징을 통해, 정방향 탐색, 역방향 탐색의 비용이 동일함.
- 페이지 식별자는 정수로, URL은 알파벳 순서로 정렬된다고 가정.
- 동일한 도메인의 페이지들이 가까운 위치에 배치되어 지역성이 페이지 식별자의 근접성으로 이어짐.
k²-Tree 구조

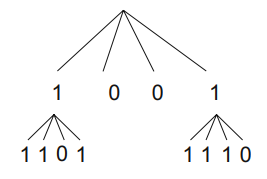
*전체 행렬의 크기 n*n과 분할 계수 k가 주어졌을 때
- 트리의 높이
- 트리의 높이인 h = $\left \lceil log_k(n)\right \rceil$
트리의 노드최고 높이의 노드를 제외한 트리의 각 노드는 서브 행렬을 표현하며, 서브 행렬 내에 1이 존재하면 해당 노드에 1을 할당, 1이 존재하지 않으면 0을 할당.
- 트리의 높이인 h = $\left \lceil log_k(n)\right \rceil$
- 서브 행렬의 크기 s = $\frac{n^{2}}{k^{2}}$
- 서브 행렬의 크기는 s 이며 재귀적으로 서브 행렬을 만들어 말단 노드가 될 때 까지 계속됨.
- n이 k의 거듭 제곱이 아닌 경우
- 행렬의 너비를 $k^{\left \lceil log_k(n)\right \rceil}$ 크기로 확장 후, 행렬의 확장된 공간에 0을 채움
k²-Tree 의 탐색 방법
정 방향 탐색 방법
p 페이지가 가리키는 페이지들을 탐색하기 위해, 인접 행렬의 p번째 행의 값들을 확인해야 함.
탐색은 트리의 루트 노드로부터 하강하며 k개의 자식 노드를 선택함.

- 첫 번째 페이지가 가리키는 페이지의 정보는 인접 행렬에서 첫 번째 행에 존재하므로, 근 노드의 첫 번째, 두 번째 노드를 확인해야 함.
- 근 노드의 첫 번째 자식의 값은 1이므로 자손 노드를 가지고, 그 자손 노드들의 높이가 최대이므로 노드들은 잎 노드로서 인접 행렬의 값들과 동일.
- 인접 행렬의 첫번째 행 값을 나타내는 잎 노드의 첫 번째와 두 번째값을 통해 첫 번째 페이지가 참조하는 페이지 값들을 확인.
- 근 노드의 두 번째 자식의 값은 0 이므로 자손 노드를 가지지 않고, 이는 해당 영역에는 1이 없음을 의미함.
- 최종적으로 첫 번째 페이지가 참조하는 페이지는 자기 자신과 두 번째 페이지
역 방향 탐색 방법
어떤 페이지들이 p 페이지를 참조하고 있는지 확인하기 위해, 인접 행렬의 p행이 아닌 p번째 열을 확인하면 됨.
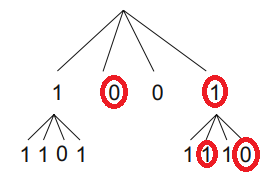
트리에서 마지막 페이지를 참조하는 페이지들을 찾는 과정.
- 마지막 페이지를 참조하는 페이지들의 정보는 인접 행렬에서 마지막 열에 존재하므로, 근 노드의 두 번째, 네 번째 노드를 확인해야 함.
- 근 노드의 두 번째 자식의 값은 0이므로 자손 노드를 가지지 않고 이는 두 번째 노드가 지니는 인접행렬의 영역에는 1이 없음을 의미.
- 근 노드의 네 번째 자식의 값은 1이므로 자손 노드를 가지고 그 자손노드들의 높이는 트리의 최대 높이와 같으므로 잎 노드로서 인접 행렬의 값들과 동일.
- 따라서 잎 노드에서 인접행렬의 마지막 열에 해당하는 값인 두 번째와 네 번째 값을 통해 마지막 페이지를 참조하는 페이지는 세 번째 페이지임을 알 수 있다.
데이터 구조와 알고리즘
- 일반적으로 N개의 노드로 이루어진 압축된 트리를 이론적 최소 비트 수로 표현할 때 2N+o(N)에 가까워짐.
- K^2 트리의 경우, 노드의 자식 수가 k 혹은 0인 경우가 많기 때문에, N+o(N)비트로 표현 가능.
데이터 구조
- 인접 행렬을 k^2 트리를 통해 두 개의 비트 배열로 표현할 수 있다.
- T(tree)배열 : 잎 노드의 비트들을 제외한 모든 내부 노드의 비트를 저장한다.
- L(leaves)배열 : 트리의 마지막 계층의 비트들을 저장. 즉 인접 행렬의 값들을 저장한다.
- 이러한 비트 구조는 배열에서 1부터 i번째 위치까지 등장한 “1”의 개수를 계산해주는 rank 쿼리를 효율적으로 사용가능.
비트 배열을 통해 노드의 자식 찾기
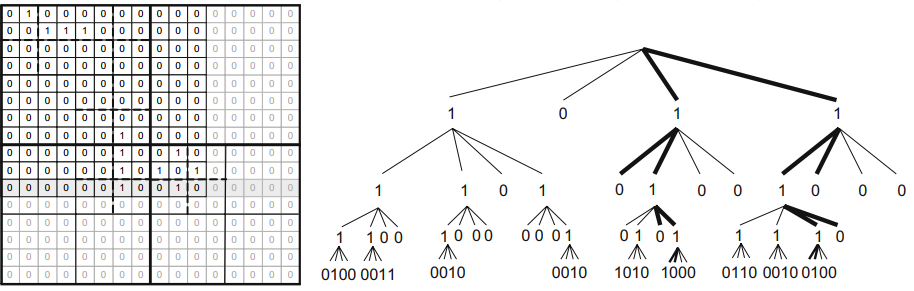
위의 K^2 트리 구조를 비트로 표현하면 다음과 같음.
T = 1011 1101 0100 1000 1100 1000 0001 0101 1110
L = 0100 0011 0010 0010 1010 1000 0110 0010 0100
T 배열에서 처음 4개의 비트는 0부터 3번째 노드로, 루트 노드의 자식들을 나타낸다. 그리고 그 다음 4개의 비트는 0 노드의 자식들을 나타내며 그 다음 4개의 비트는 1번 노드의 자식이 아닌 2번 노드의 자식들을 나타낸다. ( 1번 노드의 경우 비트 값이 0이므로 자식이 없음.)
T에서 노드 x의 i번째 자식의 위치를 나타내는 공식은 다음과 같음.

루트노드의 세번째 노드의 1번째 자식의 위치를 나타내는 과정
- 찾으려는 자식의 위치를 비트 배열에서 인덱스를 통해 찾기 위해 rank값을 계산해야 함. rank(T,2) = 2
- 그리고 1을 가진 각 노드는 4개의 자손을 가지기 때문에 rank(T,2)에 k^2 값을 곱해서 탐색 시작 위치를 찾음.
- 그리고 i번째 자식의 값을 찾기 위해 i를 더함
- 최종적으로 2*4 + 1로, L 비트 배열에서 9번째 비트인 1이 노드 2의 첫 번째 자식의 값을 나타낸다.
더 나아가 이전 노드의 3번째 자식의 위치를 찾아보면
rank(T,9) * k^2 + 3 = 7 * 4 + 3 = 31로 1을 얻을 수 있다.
또 다시 이전 노드의 0 번째 자식의 위치를 얻으면
- rank(T,31) * k^2 + 0 = 14 * 4 + 0 = 56으로 T 배열의 범위를 넘어섬.
- 이 때, 56에서 T배열의 크기인 36을 빼주면 20이 남고
- L에서 20번째 비트가 31번째 노드의 0번째 비트임을 알 수 있다. 그리고 이 값은 L 배열에 있으므로, 인접행렬의 값과 동일하다.
혼합 접근법
- K의 값이 증가할 수록 트리의 높이는 감소하여 노드 방문 횟수는 감소함.
- 노드당 k^2개의 자식노드를 가지기 때문에
- 하지만 그 반대로 잎 노드에 할당 되는 불필요한 비트수가 많아짐.
- 예를 들어 4*4 행렬에 1이 하나 있더라도, k 값이 4라면 “1”값을 저장하기 위해 불필요한 “0”값을 15개 더 저장해야함.
- 이를 개선하기 위해 계층을 증가 시킬 수록(높이가 높아질 수록) k값을 낮추는 방법을 고안할 수 있음.
- 이 방법을 통해 특정 노드의 이웃 값들을 더 빠르게 탐색할 수 있고, 잎 노드에 많은 비트 수를 할당할 필요가 없어짐.
확장된 기능
- 기존의 압축 그래프 표현들은 주로 페이지의 정방향 이웃 또는 역방향 이웃을 찾는데 중점.
- k^2트리는 그 이상의 복잡한 질의를 효율적으로 처리할 수 있는 기능 제공.
- 특정 페이지가 다른 페이지를 가리키는지 여부 확인
- 페이지 p가 페이지 q를 가리키는지 확인하려면 다른 그래프 표현들은 페이지p의 모든 정방향 이웃을 추출 하고, 그 중에서q가 있는지 확인해야함.
- k^2는 트리의 레벨을 내려가면서 자식 노드 하나로만 이동하면서 질의를 처리할 수 있음.
- 특정 범위 내 정방향 이웃 및 역방향 이웃 찾기
- 특정 페이지 p가 특정 범위 [q1, q2]에 있는 페이지들을 참조하는지 혹은 참조 받는지 확인할 수 있음.
- 두 범위 안의 모든 링크 찾기
- 앞서 서술한 질의들을 일반화 한 형태.
- 특정 페이지가 다른 페이지를 가리키는지 여부 확인
'논문 리뷰 > 데이터베이스' 카테고리의 다른 글
| Trinity 데이터베이스 예제 실행 (0) | 2024.11.05 |
|---|---|
| [논문 리뷰] TRINITY : A Fast Compressed Multi-attribute Data Store (0) | 2024.11.05 |
| [논문 리뷰] A New Method To Index And Store Spatio-temporal data (0) | 2024.10.10 |