728x90
반응형
문제 링크
https://www.acmicpc.net/problem/5557문제 요약
1학년 상근이는 숫자가 주어졌을 때 마지막 숫자와 등호(=)를 사용하여 올바른 등식을 만들고 싶어 한다. 이때 각 숫자 사이에 덧셈(+) 또는 뺄셈(-) 연산을 넣어 연산을 수행해야 한다. 중간 계산 값은 0 이상 20 이하 범위에 있어야 하며, 이를 벗어나면 올바르지 않은 등식이 된다. 목표는 주어진 숫자 배열을 사용하여 상근이가 만들 수 있는 올바른 등식의 개수를 구하는 것이다.
푼 방법
DP(동적계획법)으로 풀었습니다.
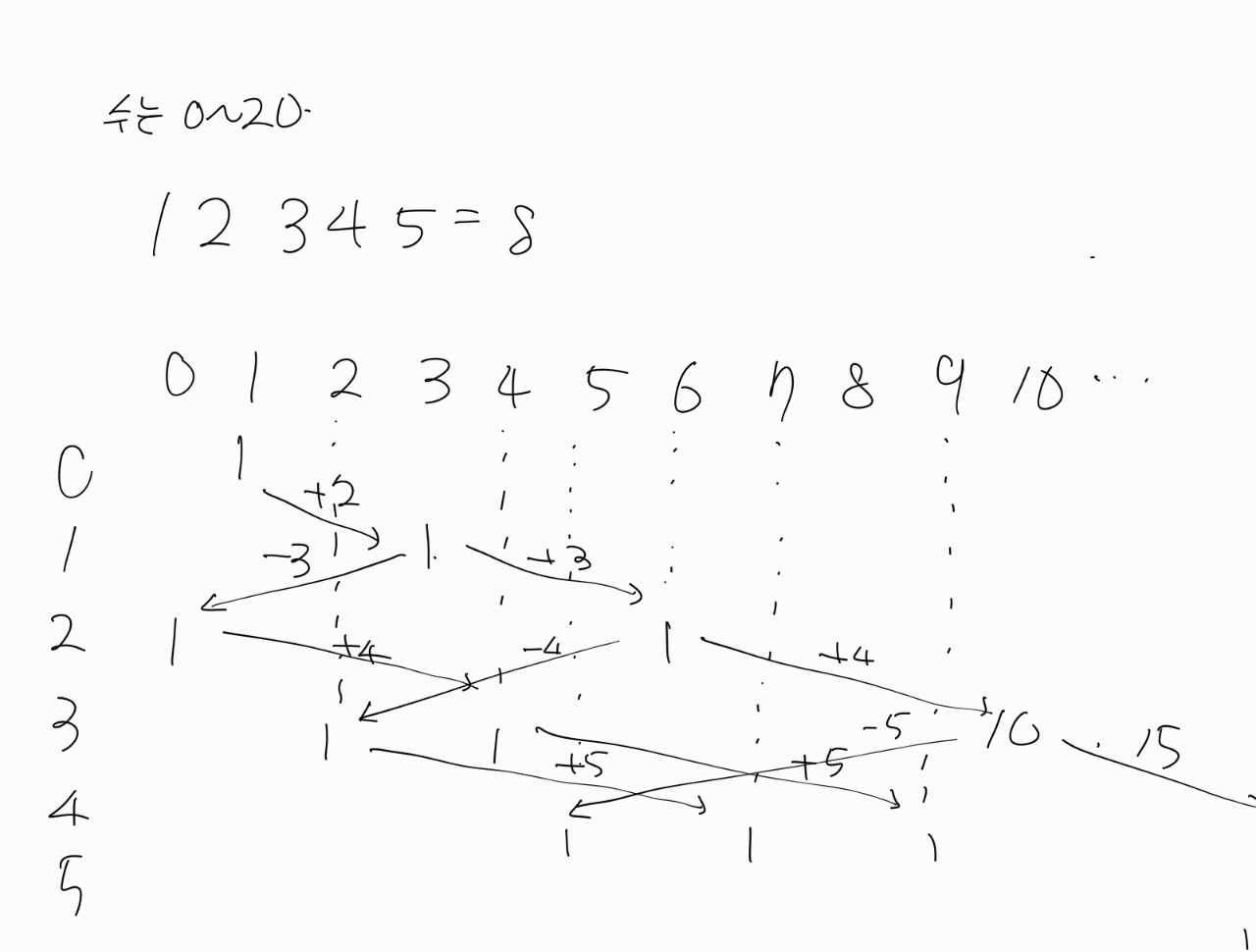
- dp[i][j]는 i번째 숫자까지 계산했을 때 j의 값이 나올 수 있는 경우의 수를 의미한다.
- 초기 조건으로 dp[0][nums[0]] = 1로 설정하여 첫 번째 숫자가 나올 수 있는 유일한 경우의 수를 반영한다.
- 각 숫자와 계산된 중간 값을 기반으로 다음 위치에서 덧셈 또는 뺄셈을 수행하며 0~20 범위 내에 속하는 경우만 dp[i][j]에 기록한다.
- 마지막 숫자 전까지 반복하여 계산한 후, 최종적으로 dp[n-2][nums[-1]]에 저장된 값을 출력한다.
정답 코드
import sys
n = int(sys.stdin.readline().rstrip())
nums = list(map(int, sys.stdin.readline().split()))
dp = [[ 0 for _ in range(21)] for _ in range(n)]
dp[0][nums[0]] = 1
for i in range(1, n-1):
for j in range(21):
if dp[i-1][j] > 0:
if j + nums[i] <= 20:
dp[i][j+nums[i]] += dp[i-1][j]
if j - nums[i] >= 0:
dp[i][j-nums[i]] += dp[i-1][j]
print(dp[n-2][nums[-1]])배웠던 부분
- 여기에 배운 내용을 나열하세요.
- 예: 새로운 알고리즘 패턴, 최적화 방법
728x90
반응형
'코딩테스트 > 백준' 카테고리의 다른 글
| [백준] 14676 영우는 사기꾼? (1) | 2024.11.16 |
|---|---|
| [백준] 25635 - 자유 이용권 (1) | 2024.11.14 |
| [백준] 14569 시간표 짜기 (0) | 2024.11.10 |
| [백준] 4179 - 불! (1) | 2024.11.09 |
| [백준] 27923 햄버거최대 몇개드실수있나요? (0) | 2024.11.08 |